Square Footage Calculator
The Square Footage Calculator online is an essential tool for homeowners, contractors, and designers. It simplifies measurements for house building, painting, and flooring, making projects more efficient and cost-effective.
Ellipse
Mastering Ellipse Square Footage: A Comprehensive Guide
From designing a picturesque garden patio to undertaking a sophisticated architectural project, the ability to accurately calculate the area of an ellipse is a surprisingly practical skill. This guide provides a clear, step-by-step approach to calculating the square footage of any elliptical shape using two simple measurements. We’ll delve into the formula, its real-world applications, and answer common questions to help you master this essential geometric calculation.
Understanding the Basics: What is an Ellipse?
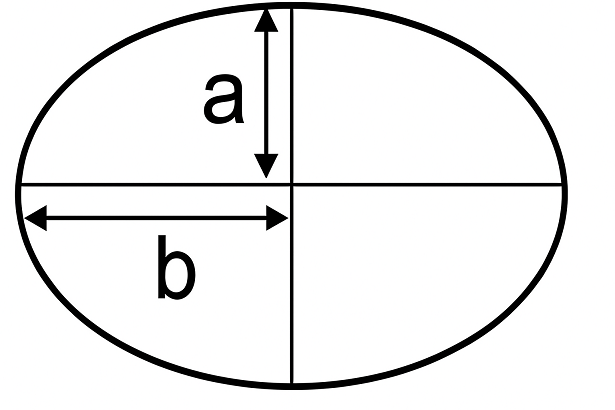
An ellipse is essentially a stretched or "squashed" circle. Where a circle has a single, constant radius, an ellipse has two distinct axes that define its shape:
- The Major Axis: The longest diameter of the ellipse.
- The Minor Axis: The shortest diameter of the ellipse, perpendicular to the major axis.
To calculate the area, we don't use the full axes but rather their halves, known as the semi-major axis and the semi-minor axis.
- Semi-Major Axis (a): Half the length of the major axis. This is the distance from the center to the furthest point on the ellipse.
- Semi-Minor Axis (b): Half the length of the minor axis. This is the a from the center to the closest point on the ellipse.
Think of 'a' as the "long radius" and 'b' as the "short radius" of your ellipse.
The Formula for the Area of an Ellipse
The formula to calculate the area of an ellipse is both simple and elegant:
A = π · a · b
Where:
- A is the Area.
- π (Pi) is the mathematical constant approximately equal to 3.14159.
- a is the length of the semi-major axis.
- b is the length of the semi-minor axis.
This formula is a beautiful extension of the area of a circle (A = πr²). In a circle, the semi-major and semi-minor axes are equal (a = b = r), so the ellipse formula naturally becomes π · r · r, or πr².
Step-by-Step Guide to Calculating Ellipse Square Footage
Calculating the area of an elliptical space is straightforward. Follow these simple steps:
Step 1: Measure the Major and Minor Axes
First, identify the longest and shortest diameters of your ellipse.
- Measure the full length of the longest part of the ellipse. This is your major axis.
- Measure the full length of the shortest part of the ellipse, ensuring your measurement is perpendicular to the major axis. This is your minor axis.
Step 2: Calculate the Semi-Major and Semi-Minor Axes (a and b)
Once you have the full axis measurements, simply divide each by two to find your 'a' and 'b' values.
- Semi-major axis (a) = Major Axis / 2
- Semi-minor axis (b) = Minor Axis / 2
Step 3: Apply the Area Formula
Now, plug your 'a' and 'b' values into the area formula: A = π · a · b.
- Multiply 'a' by 'b'.
- Multiply the result by π (approximately 3.14159).
The result is the square footage of your ellipse.
Example Calculation:
Let's say you are planning an elliptical lawn in your backyard.
- Step 1: You measure the longest part of the desired lawn area to be 20 feet (the major axis) and the shortest part to be 14 feet (the minor axis).
- Step 2: You calculate the semi-axes:
- a = 20 feet / 2 = 10 feet
- b = 14 feet / 2 = 7 feet
- Step 3: You apply the formula:
- A = π · 10 ft · 7 ft
- A = 70π sq ft
- A ≈ 219.91 sq ft
You will need approximately 220 square feet of sod for your new lawn.
Practical Applications: Where is Ellipse Area Calculation Used?
Calculating the area of an ellipse is not just a math problem; it's a practical tool for various projects:
- Landscaping and Garden Design: Perfect for determining the amount of sod for an elliptical lawn, pavers for a patio, or mulch for a garden bed.
- Interior Design: Essential for planning the placement of an elliptical rug or a custom-built dining table to ensure it fits the space.
- DIY Home Projects: Useful when creating elliptical mirrors, tabletops, or painting an elliptical design on a wall or ceiling.
- Architecture and Construction: Architects use this calculation for designing elliptical rooms, windows, atriums, and arches, which is crucial for material estimation and cost analysis.
- Swimming Pool Construction: Calculating the surface area of an elliptical pool is necessary to determine the amount of plaster or liner required and to purchase the correct size pool cover.
Frequently Asked Questions
- How do I calculate the square footage of an ellipse?
- To calculate the square footage of an ellipse, use the formula: Area = pi timesa timesb, where 'a' is the semi-major axis and 'b' is the semi-minor axis, both in feet.
- What is the formula for area of an ellipse in square feet?
- The area of an ellipse is calculated using Area = pi timesa timesb. If your dimensions are in feet, the result will be in square feet.
- How do I convert inches to feet when calculating ellipse area?
- To convert inches to feet, divide the number of inches by 12. For example, 24 inches is 2 feet.
- Can I calculate ellipse area with diameter instead of radius?
- Yes. Divide the diameters by 2 to get the semi-major and semi-minor axes, then apply the formula: Area = pi timesa timesb.
- Is the area of an ellipse larger than a circle of the same width?
- Yes, if the ellipse is elongated along the major axis, it will cover more area than a circle with the same minor axis.
- What is the difference between a major and minor axis in an ellipse?
- The major axis is the longest diameter of the ellipse, and the minor axis is the shortest. Each axis is divided by two to get 'a' and 'b' for area calculations.
- How accurate is the ellipse area calculator?
- Ellipse area calculators are very accurate if you input the correct dimensions and unit conversions.
- What unit should I use for inputting dimensions in an ellipse calculator?
- Use the same unit for both axes (e.g., feet, meters, inches). Most calculators convert the result to square feet or square meters.
- Can I use an ellipse calculator for landscaping design?
- Yes, calculating the area of an elliptical lawn or patio helps estimate materials and costs for landscaping.
- How do I calculate cost if I know the area of an ellipse?
- Multiply the square footage by the cost per square foot of the material you're using (e.g., concrete, tiles, turf).
- Is the ellipse area formula the same as for a circle?
- No. The area of a circle is pi timesr 2 . The area of an ellipse is pi timesa timesb.
- What shape is an ellipse similar to?
- An ellipse is similar to a stretched or compressed circle, like the shape of a running track or a flattened ball.
- Can I use ellipse area calculation for an oval pool?
- Yes, an oval pool is typically an ellipse, so you can use the ellipse formula to estimate surface area or cover size.
- Do I need a calculator to find the area of an ellipse?
- While you can calculate it manually using Area = pi timesa timesb, a calculator makes the process faster and reduces error.
- How do I measure the axes of an ellipse on-site?
- Use a tape measure to find the longest and shortest dimensions across the ellipse, then divide each by 2 to get 'a' and 'b'.
- Why is pi used in the ellipse area formula?
- pi is used because an ellipse is a curved shape related to a circle, and pi helps measure curved geometry.
- Can I use a laser measurer to get dimensions for ellipse area?
- Yes, laser measurers are great for getting accurate distances, especially for large ellipses.
- Can I use decimals for axis values in an ellipse calculator?
- Yes, decimals provide more precise results, especially for professional or commercial calculations.
- Do I need to round off the final square footage?
- For practical purposes like flooring or painting, rounding to two decimal places or the nearest whole number is acceptable.
- What’s the easiest way to find the area of an elliptical garden?
- Measure the longest and shortest widths, divide by 2 to get 'a' and 'b', and plug into the formula Area = pi timesa timesb.
- What is a real-life example of an elliptical area?
- Examples include elliptical driveways, oval tables, elliptical ceiling domes, and running tracks.
- Can I use an ellipse calculator for commercial tiling projects?
- Absolutely. It helps estimate square footage and materials needed for large elliptical tiled floors.
- What if I measure the ellipse wrong?
- Incorrect measurements lead to inaccurate area. Always double-check values before calculating.
- What are the input units in an ellipse area calculator?
- You can enter inputs in feet, meters, inches, or any consistent unit as long as both axes use the same one.
- Can I calculate ellipse area in square meters?
- Yes. Ensure your axis lengths are in meters, and the result will be in square meters.
- What is the area of an ellipse with a=5ft and b=3ft?
- Using Area = pi timesa timesb: Area = 3.1416 times5 times3=47.12 square feet.
- Is ellipse area used in civil engineering?
- Yes, especially in designing pathways, water bodies, seating areas, and elliptical domes.
- How to calculate the area of an elliptical table top?
- Measure the longest and shortest diameters, divide by 2, then apply Area = pi timesa timesb.
- Why are there two axes in an ellipse?
- Unlike a circle, an ellipse has unequal diameters, which define its width (minor axis) and length (major axis).
- Can I use the same calculator for a circular area?
- Yes, if both axes are equal (a = b), the ellipse becomes a circle, and the calculator will still work.
- What are common mistakes when calculating ellipse square footage?
- Common mistakes when calculating ellipse area include confusing the major and minor axes, failing to divide diameters by two to get semi-axes, using inconsistent units (e.g., mixing feet and inches), and premature rounding of Pi ( pi) or intermediate results. Always double-check your measurements and formula application.