Mastering Parallelogram Area: Understanding Square Footage with Base and Height

Imagine a familiar shape like a rectangle, then imagine pushing it over slightly, so its sides remain parallel but its corners are no longer square. You've just pictured a parallelogram. These versatile four-sided figures appear in countless aspects of our world, from architectural designs and engineering components to everyday objects and even abstract art.

Calculating the square footage or area of a parallelogram is a fundamental geometric skill. Unlike a rectangle, where any side can be its height, a parallelogram requires a specific understanding of its dimensions: its base and its perpendicular height. This comprehensive guide will break down the simple yet powerful formula for parallelogram area, explain the crucial concept of perpendicular height, walk you through step-by-step examples, and illuminate the many practical applications of this knowledge. By the end, you'll be able to confidently determine the area of any parallelogram given its essential measurements.

I. What is a Parallelogram? Understanding Its Unique Properties

Before diving into area calculations, let's clearly define what a parallelogram is and what makes it distinct.

A parallelogram is a flat, four-sided shape (a quadrilateral) where opposite sides are parallel and equal in length. This parallelism gives the parallelogram its characteristic "slanted" appearance compared to a rectangle.

Key properties that define a parallelogram include:

• Opposite Sides are Parallel: This is the defining characteristic. If you extend any pair of opposite sides, they will never intersect.
• Opposite Sides are Equal in Length: The length of one side is equal to the length of its opposite side.
• Opposite Angles are Equal: The angles directly across from each other are identical in measure.
• Consecutive Angles are Supplementary: Any two angles that share a side add up to 180 degrees. For example, if one angle is 70°, the adjacent angle will be 110°.
• Diagonals Bisect Each Other: The lines connecting opposite vertices intersect at their midpoints.

How does a parallelogram relate to other quadrilaterals?

It's helpful to see parallelograms in context:

• Rectangle: A special type of parallelogram where all four angles are right angles (90°).
• Rhombus: A special type of parallelogram where all four sides are equal in length.
• Square: A special type of parallelogram that is both a rectangle (all angles are 90°) and a rhombus (all sides are equal).

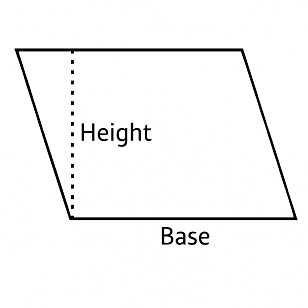
In the context of area, we are interested in two specific dimensions of a parallelogram:

• Base (b): Any one of the parallelogram's sides can be chosen as the base.
• Height (h): This is the crucial dimension. The height is the perpendicular distance between the chosen base and the side parallel to it. It is not necessarily the length of the slanted side. Imagine dropping a straight line from one vertex down to the base (or an extension of the base) such that it forms a 90-degree angle. That line's length is the height.

Understanding these properties is essential for correctly identifying the base and height, which are the only two inputs needed for the area formula.

II. The Fundamental Formula for Parallelogram Area: Base × Height

The area of any two-dimensional shape represents the amount of space it covers. For a parallelogram, this calculation is surprisingly simple once you grasp the concept of perpendicular height.

• The Formula:

  Area = base × height

  Or, more commonly written as:

  A = b × h

  Where:

  • A = Area of the parallelogram
  • b = Length of the chosen base
  • h = Perpendicular height corresponding to that base
• Understanding the Logic: Why does it work? (The Transformation Method)

The formula A = b × h might seem less intuitive than length times width for a rectangle, especially with the "slanted" nature of a parallelogram. However, its validity becomes clear through a simple visualization:

1. Start with a Parallelogram: Imagine a parallelogram drawn on a piece of paper.
2. Draw the Height: From one of the top vertices, draw a straight, perpendicular line down to the base. This forms a right-angled triangle at one end of the parallelogram.
3. Cut and Rearrange: Now, imagine carefully cutting off this right-angled triangle from one end of the parallelogram.
4. Move the Triangle: Take the cut-off triangle and move it to the other end of the parallelogram, fitting it perfectly against the other slanted side.
5. Behold, a Rectangle! What you now have is a perfect rectangle. The length of this rectangle is the same as the base (b) of your original parallelogram. The width of this rectangle is the same as the perpendicular height (h) of your original parallelogram.

Since the area of a rectangle is simply its length times its width, and we've demonstrated that a parallelogram can be transformed into a rectangle with equivalent base and height dimensions, it logically follows that:

A_{parallelogram} = A_rectangle = length × width = b × h

This visual proof simplifies what might otherwise seem like a complex geometric problem.

Units of Area:
When calculating area, your units will always be "square units." If your base is in meters and your height is in meters, your area will be in square meters (m²). If your base is in feet and your height is in feet, your area will be in square feet (ft²), also known as square footage. It's crucial to ensure your base and height measurements are in consistent units before you multiply them.

III. Step-by-Step Calculation Examples

Let's apply the formula with some practical examples to solidify your understanding.

Example 1: Basic Area Calculation

Problem: A parallelogram has a base of 12 centimeters and a perpendicular height of 7 centimeters. What is its area?

Solution:

1. Identify given values:
   • Base (b) = 12 cm
   • Height (h) = 7 cm
2. Choose the correct formula: The area of a parallelogram is A = b × h.
3. Substitute values:

   A = 12 cm × 7 cm

4. Calculate:

   A = 84 cm²

Answer: The area of the parallelogram is 84 square centimeters.

Example 2: Finding a Missing Dimension (Height)

Problem: A parallelogram has an area of 56 square feet. If its base is 8 feet, what is its perpendicular height?

Solution:

1. Identify given values:
   • Area (A) = 56 ft²
   • Base (b) = 8 ft
2. Choose and rearrange the formula: We know A = b × h. To find the height, we can rearrange this to h = A / b.
3. Substitute values:

   h = 56 ft² / 8 ft

4. Calculate:

   h = 7 ft

Answer: The perpendicular height of the parallelogram is 7 feet.

Example 3: Dealing with Different Units (Conversion Required)

Problem: A piece of sheet metal is shaped like a parallelogram. Its base measures 2.5 meters, and its perpendicular height is 75 centimeters. What is the area of the metal piece in square meters?

Solution:

1. Identify given values and note unit discrepancy:
   • Base (b) = 2.5 meters
   • Height (h) = 75 centimeters
2. Perform Unit Conversion: To calculate the area in square meters, we must convert the height from centimeters to meters.
   • Since 1 meter = 100 centimeters,
   • 75 cm = 75 / 100 m = 0.75 m
3. Choose the correct formula: A = b × h.
4. Substitute converted values:

   A = 2.5 m × 0.75 m

5. Calculate:

   A = 1.875 m²

Answer: The area of the sheet metal is 1.875 square meters.

Example 4: Parallelogram on a Coordinate Plane (Conceptual Example)

Problem (Conceptual): If a parallelogram is defined by coordinates of its vertices, how would you find its area?

Solution (Conceptual Steps):

1. Identify a Base: Choose any side as the base. You can calculate its length using the distance formula (d = √(x₂-x₁)² + (y₂-y₁)²).
2. Determine Corresponding Height: This is the trickier part. The height is the perpendicular distance from a vertex on the opposite side to the line containing the chosen base. This often involves:
   • Finding the equation of the line containing the base.
   • Finding the equation of a line perpendicular to the base line and passing through a vertex on the opposite side.
   • Calculating the intersection point of these two lines.
   • Using the distance formula again to find the distance between the vertex and the intersection point (this is the height).
   • Alternatively, using a more advanced formula involving determinants or cross products of vectors if vector math is available.

While detailed calculations for coordinate plane parallelograms are beyond a basic explanation of area, understanding that base and height can be derived from coordinates illustrates the formula's broader applicability.

IV. Practical Applications: Where Parallelogram Area Matters

The ability to calculate the area of a parallelogram is far from a mere academic exercise. It has tangible applications across various fields, enabling precise measurements and informed decision-making.

• Architecture and Construction:
  • Building Design: Architects frequently incorporate parallelogram shapes in floor plans, wall designs, or roof structures for aesthetic and functional purposes. Calculating the area helps determine material quantities for flooring, roofing shingles, insulation, or paint for these non-rectangular sections.
  • Material Estimation: For tiles, carpeting, or cladding materials that need to cover parallelogram-shaped spaces, accurate area calculations minimize waste and ensure sufficient supply.
• Engineering:
  • Structural Analysis: Engineers analyze forces and stresses on structural components. Beams, plates, or sections of bridges might have parallelogram cross-sections, and their area is crucial for calculating load distribution and material strength.
  • Mechanical Design: Components in machinery like linkages, pistons, or certain gear mechanisms often move in ways that sweep out parallelogram-shaped areas. Understanding this area is vital for designing efficient and safe mechanisms.
  • Aerodynamics/Fluid Dynamics: Calculating the area of a parallelogram-shaped wing section or a channel for fluid flow can be important for analyzing lift, drag, or flow rates.
• Manufacturing and Fabrication:
  • Pattern Cutting: Industries that cut materials like fabric, sheet metal, wood, or plastic often work with patterns that include parallelogram shapes. Accurate area calculations help optimize cutting layouts, reduce material waste, and streamline production.
  • Die Design: In stamping or pressing operations, the area of the die that forms a parallelogram shape directly impacts the force required and the material used.
• Land Surveying and Agriculture:
  • Property Measurement: While many land plots are irregular, some can be approximated or broken down into parallelograms for easier area calculation by surveyors. This is crucial for property boundaries and land valuation.
  • Crop Yield Estimation: Farmers might use parallelogram calculations for specific sections of fields to estimate crop yields or determine the amount of fertilizer or seeds needed.
• Art and Graphic Design:
  • Perspective Drawing: Artists and graphic designers use the concept of parallelograms to create realistic perspective and three-dimensional effects on a two-dimensional surface.
  • Abstract Art & Sculpture: Artists often use geometric shapes, including parallelograms, in their compositions, and understanding the area can be part of their design process.
• Everyday Life:
  • Home Improvement: Measuring areas for flooring, painting, or wallpapering a room that isn't perfectly rectangular.

V. Common Pitfalls and Tips for Accuracy

While the formula A = b × h is elegantly simple, errors often arise from misinterpreting the 'height' or overlooking unit consistency. Here are common pitfalls and tips to ensure accurate calculations:

1. Confusing Height with Side Length: This is by far the most common mistake. The height (h) is never the length of a slanted side (unless the parallelogram is a rectangle). The height must be the perpendicular distance between the chosen base and its opposite parallel side. Always visualize or draw a right angle from the top vertex to the base.
2. Inconsistent Units: Before you multiply, ensure that your base and height measurements are in the same units. If the base is in feet and the height is in inches, you must convert one to match the other (e.g., convert inches to feet or feet to inches). Forgetting this step will lead to a nonsensical area unit (e.g., foot-inches) and an incorrect numerical value.
3. Choosing the Right Base: While any side of a parallelogram can be chosen as the base, the height must be the perpendicular distance corresponding to that specific chosen base. If you switch bases, you must also use the height that is perpendicular to the new base.
4. Careless Arithmetic: Though the multiplication is simple, double-check your calculations, especially with decimals or fractions.
5. Sense Check Your Answer: After calculating, ask yourself: Does this answer make sense? If you have a parallelogram with a base of 10 units and a very small height (e.g., 0.5 units), the area should be small. If you accidentally used a slanted side of 5 units as the height, you'd get an area of 50, which would be disproportionately large for a "squashed" parallelogram. A quick mental approximation can catch significant errors.
6. Label Units Clearly: Always state your final answer with the correct square units (e.g., square meters, square feet, cm², in²). This clarifies the meaning of your numerical result.

Conclusion

The parallelogram, a quadrilateral with two pairs of parallel sides, is a ubiquitous shape in our environment. Its area, or square footage, is determined by a simple yet powerful formula: Area = Base × Height. The key to unlocking accurate calculations lies in correctly identifying the perpendicular height—the straight, shortest distance between the chosen base and its parallel opposite side.

By understanding the geometric properties of parallelograms, recognizing the intuitive transformation into a rectangle, and diligently applying the formula while being mindful of unit consistency and the distinction between slanted sides and perpendicular height, you are now equipped to tackle any parallelogram area calculation. From designing innovative structures to optimizing material usage in manufacturing, mastering the area of a parallelogram provides a fundamental tool for practical problem-solving in countless real-world scenarios.