Square Footage Calculator

The Square Footage Calculator online is an essential tool for homeowners, contractors, and designers. It simplifies measurements for house building, painting, and flooring, making projects more efficient and cost-effective.

Home FAQ.. Percentage Calculator
Age Calculator Base64 Decoder / Encoder
URL Decoder / Encoder

Modify the values and click the calculate button to use

Know More About The Individual Shapes...

Triangle with Base & Height

Triangle With Base Shape

Mastering Triangle Square Footage: A Comprehensive Guide to Area Calculation (Base and Height Method)

Understanding how to accurately calculate the square footage of a triangle is a fundamental skill with vast practical applications, from home renovations and construction to gardening, interior design, and even educational contexts. While the concept might seem simple at first glance—"half of base times height"—truly mastering it involves appreciating the nuances, common pitfalls, and the robust utility of this geometric principle. This detailed guide will delve deep into the calculation of a triangle's square footage using its base and height, providing a thorough understanding that resonates with both beginners and those seeking to refine their knowledge for optimal accuracy and efficiency.

The Core Concept: Unveiling the Triangle's Area Formula

At the heart of calculating a triangle's square footage lies a remarkably elegant and straightforward formula:

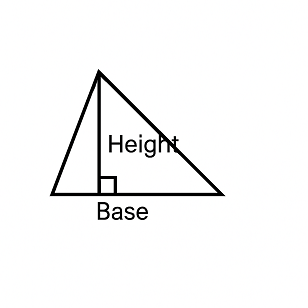
Area = (1/2) × Base × Height

Or, as it's often written:

Area = 0.5 × Base × Height

In this formula:

Area: Represents the two-dimensional space enclosed within the triangle, expressed in square units (e.g., square feet, square meters, square inches).

Base (B): Any side of the triangle can be designated as the base. It is the side to which the height is drawn.

Height (H): The perpendicular distance from the chosen base to the opposite vertex (the corner furthest from the base). The height must form a 90-degree angle with the base.

This formula works universally for all types of triangles—acute, obtuse, and right-angled—a fact we will explore in detail.

Why "Half of Base Times Height"? Visualizing the Principle

To truly grasp the formula, it's helpful to visualize its derivation. Imagine a rectangle or a parallelogram. Its area is simply calculated by multiplying its base (length) by its height (width).

Now, picture any triangle. You can always enclose this triangle within a rectangle or a parallelogram such that the triangle's base is one side of the rectangle/parallelogram, and its height is the perpendicular distance between that base and the opposite parallel side.

Consider these scenarios:

Right-Angled Triangle: A right triangle is exactly half of a rectangle. If you draw a diagonal across a rectangle, you form two identical right triangles. The area of the rectangle is Base × Height, so the area of each right triangle is (1/2) × Base × Height.

Acute or Obtuse Triangle: For other triangles, you can still construct a parallelogram (or rectangle) around them. If you make a copy of the triangle, flip it, and place it adjacent to the original, you will form a parallelogram. The area of this parallelogram is Base × Height. Since the parallelogram is made of two identical triangles, the area of one triangle must be half of the parallelogram's area, leading back to (1/2) × Base × Height.

This visual intuition solidifies the understanding that the formula is not arbitrary but deeply rooted in fundamental geometric principles.

Essential Tools and Accurate Measurement Techniques

Before you can apply the formula, accurate measurement is paramount. The precision of your square footage calculation directly depends on the precision of your base and height measurements.

Required Tools:

Tape Measure: A retractable steel tape measure (25-30 feet for rooms, longer for outdoor spaces) is essential. For greater accuracy over long distances, a laser distance measurer (LDM) is highly recommended.

Pencil and Paper/Notepad: To record measurements clearly and avoid errors.

Calculator: For performing the multiplication and division.

Straightedge/Chalk Line (Optional but Recommended for Large Areas): To ensure your "height" measurement is truly perpendicular to the "base."

Level (Optional): To ensure a flat surface for measuring if uneven terrain is an issue.

Measurement Techniques for Base and Height:

1. Choosing the Base:

Any side of the triangle can be chosen as the base. However, for practical purposes, it's often easiest to select a side that is already defined by a wall, boundary, or a straight line you can easily measure.

2. Measuring the Base (B):

Measure the chosen base length accurately from one end to the other.

For physical spaces, measure wall-to-wall, or along the edge of the area you intend to calculate.

Ensure the tape measure is taut and straight, not sagging or angled.

Record the measurement in feet. If you measure in feet and inches (e.g., 10 feet 6 inches), convert the inches to a decimal part of a foot (6 inches ÷ 12 inches/foot = 0.5 feet, so 10.5 feet).

3. Measuring the Height (H):

This is often the trickiest part, as the height must be perpendicular to the base.

For a Right-Angled Triangle: If you choose one of the legs (the sides forming the 90-degree angle) as the base, the other leg automatically serves as the height. Measure both directly.

For Acute or Obtuse Triangles:

Identify the Opposite Vertex: This is the corner directly opposite the chosen base.

Drop a Perpendicular: Imagine a line dropping straight down (or up, or sideways) from this vertex to the base, forming a perfect 90-degree angle. This imagined line represents the height.

Practical Measurement:

Place one end of your tape measure at the opposite vertex.

Extend the tape measure towards the base.

While extending, use a large carpenter's square, a level, or even a plumb bob (for vertical heights) to ensure the tape measure forms a perfect right angle with the base line.

If the perpendicular line falls outside the base (common for obtuse triangles), you'll need to extend the imaginary line of the base to meet the perpendicular height. The base measurement itself remains the original length of the triangle's side.

Tip: For large outdoor areas, you might use stakes and strings to define the base line, then measure the height from the vertex to the string at a perfect right angle.

Example Measurement & Conversion:

Let's say you measure a base as 15 feet 9 inches and a height as 8 feet 3 inches.

Base: 15 feet + (9 inches / 12) = 15 + 0.75 = 15.75 feet

Height: 8 feet + (3 inches / 12) = 8 + 0.25 = 8.25 feet

Step-by-Step Calculation Process

Once you have your accurate base and height measurements in feet, the calculation is straightforward:

Step 1: Measure the Base (B)

Identify one side of the triangle to be your base.

Measure its length in feet. Convert any inches to decimal feet.

Example: B = 15.75 feet

Step 2: Measure the Height (H)

Measure the perpendicular distance from the opposite vertex to your chosen base. Ensure it forms a 90-degree angle. Convert any inches to decimal feet.

Example: H = 8.25 feet

Step 3: Apply the Formula

Substitute your measurements into the formula: Area = 0.5 × B × H

Example: Area = 0.5 × 15.75 feet × 8.25 feet

Step 4: Calculate the Area

Perform the multiplication. The result will be in square feet (ft²).

Example: Area = 0.5 × 129.9375 = 64.96875 square feet

Step 5: Round to Practical Precision (Optional but Recommended)

For most practical applications, you won't need many decimal places. Round to two decimal places, or to the nearest whole number if extreme precision isn't required.

Example: Area ≈ 64.97 square feet or 65 square feet

Practical Applications of Triangle Square Footage

Understanding triangle area is incredibly versatile. Here are some real-world scenarios where this calculation is indispensable:

Flooring and Carpeting: For rooms with triangular sections (e.g., bay windows, attic spaces, custom designs), calculating the exact square footage ensures you buy the right amount of material, minimizing waste and cost.

Painting and Wallpapering: Estimating the surface area of triangular wall sections for paint or wallpaper.

Gardening and Landscaping: Determining the area of triangular flower beds, vegetable patches, or pond liners to calculate soil volume, plant density, or liner size.

Construction and Roofing: Calculating the area of gable ends on a house (which are typically triangular) for siding, insulation, or ventilation. Roofing sections on hip or gable roofs are often triangular or trapezoidal (which can be broken into rectangles and triangles).

Real Estate and Property Assessment: While main structures are often rectangular, unusual lot shapes or custom home designs might incorporate triangular sections, impacting overall usable area calculations.

Interior Design and Layout: Planning furniture placement or custom-built elements in irregularly shaped rooms.

Crafts and Sewing: Calculating fabric or material needs for triangular patterns.

Estimating Materials (e.g., Concrete, Mulch): Once you have the square footage, you can multiply by the desired depth (converted to feet) to find cubic feet, which can then be converted to cubic yards for bulk material orders.

Common Pitfalls and How to Avoid Them

Even with a simple formula, errors can occur. Being aware of these common mistakes will help you achieve accurate results:

Incorrect Height Measurement: This is by far the most frequent error. The height must be perpendicular to the base. Measuring a slanted side (hypotenuse) instead of the true perpendicular height will lead to incorrect results.

Inconsistent Units: Mixing feet and inches without converting inches to decimal feet will lead to significant errors. Always convert all measurements to a single unit (feet) before calculation.

Assuming Right Angles: Do not assume a corner is 90 degrees unless you've measured it or know it to be so. If it's not a right angle, using an adjacent side as 'height' will be wrong. Always measure the perpendicular height.

Rounding Too Early: Avoid rounding intermediate decimal values too much. Carry at least 3-4 decimal places throughout the calculation and only round your final answer to the desired precision.

Measurement Errors: Simple human errors like misreading the tape measure, allowing it to sag, or not measuring from a consistent point can throw off calculations. Double-check all measurements.

Complex Shapes: For irregular shapes that are not simple triangles, avoid trying to force a triangle formula. Instead, break down complex shapes into a combination of simpler polygons (rectangles, squares, and triangles) and calculate each section's area separately before summing them up.

Advanced Considerations and Related Concepts

While the base and height method is fundamental, it's worth touching upon other concepts that can enhance your understanding:

Heron's Formula: If you know the lengths of all three sides of a triangle but cannot easily measure its height, Heron's formula allows you to calculate the area. This involves finding the semi-perimeter first.

Trigonometry: For surveying or architectural applications where angles are known, trigonometric functions (like sine) can be used to determine height or area. For example, Area = (1/2)ab sin(C), where a and b are two sides and C is the included angle.

Waste Factor: When ordering materials like flooring, paint, or fabric for a triangular area, always add a "waste factor" (typically 5-15%). This accounts for cuts, errors, and material imperfections. It's better to have a little extra than to run short.

Net vs. Gross Area: In construction, sometimes "net area" (actual usable space) and "gross area" (total enclosed space, including wall thickness) are differentiated. Understand which is required for your specific application.

3D Volume Calculations: The calculated square footage of a triangular base can be the first step in calculating the volume of a 3D shape, such as a triangular prism (e.g., a ramp, a wedge) or a pyramid, by multiplying the base area by its height/depth.

Conclusion: Empowering Your Projects with Accurate Calculations

The calculation of a triangle's square footage using its base and height is an indispensable tool in a multitude of practical scenarios. By understanding the core formula, employing accurate measurement techniques, and being mindful of common pitfalls, you can confidently determine the area of any triangular space. This knowledge empowers you to make informed decisions for purchasing materials, estimating costs, and successfully completing projects, large or small. Embrace the power of geometry, and let accurate square footage calculations be the foundation of your next endeavor.

Frequently Asked Questions

What is the simplest way to calculate the square footage of a triangular space?
The simplest way to calculate the square footage of any triangle is by using the formula: Area = (1/2) × Base × Height, or 0.5 × Base × Height. This works for all types of triangles, whether acute, obtuse, or right-angled.
Why is the triangle area formula 'half of base times height'?
This formula stems from the fact that any triangle can be viewed as half of a parallelogram (or rectangle) with the same base and height. If you duplicate a triangle, flip it, and place it next to the original, they form a parallelogram whose area is Base × Height. Therefore, the single triangle's area is half of that.
What do 'base' and 'height' refer to in triangle square footage calculation?
The 'base' (B) is any side of the triangle you choose. The 'height' (H) is the perpendicular distance from the opposite vertex (corner) to that chosen base. It must form a 90-degree angle with the base.
Do I need to convert inches to feet when measuring for triangular square footage?
Yes, absolutely. To get the final area in square feet, both your base and height measurements must be in feet. Convert inches to decimal feet by dividing the inches by 12 (e.g., 6 inches = 0.5 feet).
What are the essential tools for accurately measuring a triangle's base and height?
You'll need a good quality tape measure (steel or laser distance measurer), a pencil, paper for notes, and ideally a large carpenter's square or a level to ensure your height measurement is truly perpendicular to the base.
How do I measure the height of an obtuse triangle where the height falls outside the base?
For an obtuse triangle, extend the line of the chosen base (imaginary line). The height is then the perpendicular distance from the opposite vertex to this extended base line. The actual base measurement remains the original length of the triangle's side.
Is a right-angled triangle easier to calculate square footage for?
Yes, often. If you choose one of the legs (the sides forming the 90-degree angle) as the base, the other leg automatically becomes the perpendicular height, simplifying the measurement process.
How to calculate triangular flooring area for a room with angled walls?
Identify the triangular section. Measure one side as the base and then accurately measure the perpendicular distance from the opposite corner to that base. Use Area = 0.5 × Base × Height. Remember to add a waste factor for cuts (e.g., 10-15%).
What is the common mistake in measuring triangle height for area calculation?
The most common mistake is measuring a slanted side of the triangle instead of the true perpendicular distance (altitude) from the vertex to the base. The height must always form a 90-degree angle with the base.
Can I calculate the area of a triangular garden bed for soil ordering?
Yes, measure the base and perpendicular height of your triangular garden bed in feet. Calculate the square footage using the formula. Then, multiply the square footage by the desired soil depth (in feet) to get cubic feet, and divide by 27 to get cubic yards.
How to convert square meters to square feet for a triangular area?
First, calculate the area in square meters (m²) using base and height in meters. Then, convert square meters to square feet by multiplying your m² result by 10.7639 (since 1 m² ≈ 10.7639 ft²).
When should I add a waste factor to my triangular square footage calculation?
Always add a waste factor (typically 5-15%, sometimes more for complex patterns) when purchasing materials like flooring, tiles, or fabric for any triangular area. This accounts for cuts, errors, and material loss.
How to calculate the square footage of a triangular gable end for siding or painting?
Measure the width of the house at the base of the gable (this is your base). Then, measure the vertical height from the center of the base up to the peak of the roof (this is your perpendicular height). Apply the 0.5 × Base × Height formula.
What if my room is an irregular shape, not a perfect triangle?
For irregular shapes, break them down into simpler geometric figures (rectangles, squares, and triangles). Calculate the square footage of each smaller section and then add them all together to get the total area.
How does triangle square footage impact material purchasing decisions?
Accurate triangle square footage ensures you buy precisely the right amount of material like flooring, paint, or wallpaper. This minimizes waste, reduces costs, and prevents the hassle of running short or having excessive leftovers.
Can I use an online calculator to check my manual triangle area calculations?
Yes, many free online geometry or area calculators allow you to input the base and height of a triangle to verify your manual calculations. It's a good practice for double-checking accuracy.
What are the implications of rounding errors in triangle square footage calculations?
Rounding too early in the process (e.g., during unit conversion) can lead to significant cumulative errors, especially for large areas. It's best to carry at least 3-4 decimal places throughout the calculation and only round your final answer.
How is triangular square footage used in real estate property assessment?
While main structures are typically rectangular, triangular sections of a home or oddly shaped land plots are included in the overall calculation of usable or assessed square footage, impacting property value.
What's the difference between an acute, obtuse, and right triangle in terms of area calculation?
The formula (0.5 × Base × Height) is the same for all. The difference lies in how the height is physically measured: it's one of the legs for a right triangle, falls inside for an acute triangle, and may fall outside (on an extended base line) for an obtuse triangle.
Can I choose any of the three sides as the base for the calculation?
Yes, you can. No matter which side you designate as the base, as long as you measure the correct perpendicular height from the opposite vertex to that base, the calculated area will be the same.
How accurate should my measurements be for a triangle's square footage?
For most home projects, measuring to the nearest inch or half-inch is usually sufficient. For large, expensive, or professional projects, striving for quarter-inch or even millimeter precision is recommended to minimize errors and waste.
What are the common units for triangle area in construction and home improvement?
The most common unit is square feet (sq ft or ft²). Sometimes square yards are used, particularly for outdoor materials, where 1 square yard equals 9 square feet.
How do I calculate the area of a triangular section of roofing?
Measure the base of the triangular section along the eave or ridge. Then measure the perpendicular distance from the opposite peak or corner down to that base. Apply Area = 0.5 × Base × Height, and account for roofing waste factor.
Can this formula be used for very small triangles, like in crafts?
Yes, the formula applies to any size triangle. For very small items, you might measure in inches or centimeters, and then the result will be in square inches or square centimeters. Convert to square feet if needed (1 sq ft = 144 sq inches).
What if the triangular area has obstructions like columns or irregular corners?
Calculate the total triangular area first. Then, measure the area of any obstructions or irregular cutouts (e.g., a small rectangular column) and subtract their square footage from the total. For alcoves, calculate and add their area.
How does triangle square footage help in estimating paint quantities?
Once you have the square footage of the triangular wall section, divide it by the paint's coverage rate (e.g., 350-400 sq ft per gallon). This tells you how many gallons you need, ensuring you account for multiple coats.
Is 'altitude' the same as 'height' in triangle area calculations?
Yes, 'altitude' is another term for the height of a triangle. It refers to the perpendicular line segment from a vertex to the line containing the opposite side (the base).
How do I measure the base of a triangle if it's not along a straight wall?
If the base is not a defined structural element, you can use a chalk line, string, or a long straightedge to establish a straight line between the two vertices that define your chosen base, and then measure along that line.
What are the common errors when converting mixed units (feet and inches) for triangle area?
The most common error is treating inches as decimal points (e.g., 10 feet 6 inches becomes 10.6 feet). Always divide inches by 12 (6 inches / 12 = 0.5 feet, so 10 feet 6 inches = 10.5 feet).
How can I verify if my calculated triangle square footage is correct?
Double-check your original measurements. Recalculate using a calculator. Use an online triangle area calculator as a cross-reference. For irregular shapes, consider breaking them down differently or using multiple measuring methods.
Does the type of material (e.g., wood, fabric, concrete) affect the area calculation?
No, the physical material of the triangle does not affect its two-dimensional square footage. The formula applies universally to the geometric shape itself.
How to calculate the cost of a triangular piece of material if I know the price per square foot?
First, calculate the square footage of the triangular piece (including any waste factor if applicable). Then, multiply the total square footage by the price per square foot of the material.
Why is perpendicularity crucial for height measurement?
Perpendicularity (forming a 90-degree angle) is crucial because it ensures you are measuring the shortest and most direct distance from the vertex to the base. Any deviation will result in an inaccurate (typically overestimated) height and thus an incorrect area.
What is the formula if I only know the three side lengths of a triangle?
If you know all three side lengths (a, b, c), you can use Heron's formula. First, calculate the semi-perimeter (s = (a + b + c) / 2). Then, Area = √[s(s - a)(s - b)(s - c)].
Can laser distance measurers improve accuracy for triangular areas?
Yes, laser distance measurers (LDMs) can significantly improve accuracy, especially over longer distances or when measuring alone. They reduce human error from tape sagging or misreading, but you still need to ensure perpendicularity for the height.
How to break down a complex, irregular room shape that includes triangles?
Sketch the room layout. Divide it into the largest possible simple shapes: rectangles, squares, and right triangles. Measure each individual section, calculate its area, and then sum all the individual areas to get the total.
Does the height of the triangle need to be inside the triangle?
No, the height does not always need to be inside the triangle. For acute triangles, it will be inside. For right triangles, it's one of the legs. For obtuse triangles, the perpendicular height may fall outside the triangle on the extended line of the base.
How many square inches are in one square foot?
There are 144 square inches in one square foot (since 1 foot = 12 inches, 1 sq ft = 12 inches × 12 inches = 144 sq inches).
What is the relationship between the perimeter of a triangle and its area?
There is no simple, direct formula that universally links a triangle's perimeter to its area for all triangles. While both are properties of the triangle, knowing one does not automatically give you the other without additional information about the shape.
Can square footage be negative?
No, square footage represents a physical area and is always a non-negative value. It can be zero if there is no area, but never negative.
How do architects use triangular square footage calculations?
Architects use it for space planning, optimizing designs for triangular sections, calculating material quantities for specific structural or aesthetic elements (e.g., roof eaves, custom windows), and ensuring adherence to building codes.
What are common real-world applications for triangular square footage?
Common applications include calculating areas for flooring, painting, roofing, landscaping (garden beds), custom carpentry, real estate valuation, and estimating material costs for various construction projects.
How to calculate the volume of a triangular prism using square footage?
First, calculate the square footage of the triangular base using 0.5 × Base × Height. Then, multiply this base area by the height (length) of the prism itself to get the volume in cubic feet.
What are best practices for recording triangle measurements?
Draw a rough sketch of the triangle, clearly label the base and height, and write down your measurements immediately. Double-check measurements before leaving the site, and use consistent units throughout.
Does a triangular room's square footage account for doorways or openings?
For floor area, you typically calculate the full square footage as if the doorway is part of the room, as material extends into the threshold. For wall area (e.g., painting), you would subtract the area of any significant openings like doors or windows.
How does square footage relate to linear feet for triangular shapes?
Linear feet measure a single dimension (e.g., for trim or baseboards around the perimeter of a triangle). Square footage measures a two-dimensional area. They are distinct measurements, though the side lengths (linear feet) are used to calculate the area (square feet).
Can an oddly shaped piece of land be calculated using triangle square footage?
Often, oddly shaped land plots can be divided into a series of triangles and possibly rectangles or trapezoids. Calculate the area of each component, then sum them up for the total land area. Professional surveyors typically handle complex land plots.
How do I ensure a straight base line when measuring a large outdoor triangular area?
Use two stakes and a taut string line to establish a perfectly straight base. Then, you can measure along the string. For perpendicularity, use a large carpenter's square or the 3-4-5 rule (creating a right triangle with sides 3, 4, and 5 units long) at the base to set up your height measurement.
Is there a specific online tool recommended for triangle square footage calculations?
While I cannot recommend a specific external tool, searching for 'triangle area calculator' on Google will yield numerous free, user-friendly options where you can input base and height.
What are the limitations of the base and height method for triangle area?
The main limitation is the difficulty in accurately measuring the perpendicular height in real-world scenarios, especially for irregular or complex shapes. If height is hard to obtain, using Heron's formula (requiring all three side lengths) might be a better alternative.
How do I calculate the area of a triangular section of drywall for installation?
Measure the desired base of the drywall section and its corresponding perpendicular height. Apply the formula 0.5 × Base × Height. Remember to add a waste factor (typically 10-15%) for cuts and potential errors.
Does the pitch or slope of a triangular roof affect its surface area calculation?
Yes, the pitch or slope directly determines the height of the triangular roof section, which is critical for its surface area. A steeper pitch means a greater height for a given base, resulting in a larger surface area to cover with roofing materials.
How do I calculate the square footage for triangular concrete slabs?
Measure the base and perpendicular height of the triangular slab area in feet. Use Area = 0.5 × Base × Height to get the square footage. This square footage is then used with the desired slab thickness to calculate cubic yards of concrete needed.
What if the triangle is very narrow and long?
The formula remains the same. However, measuring the perpendicular height accurately for a very narrow triangle can be challenging. Ensure your perpendicular measurement is precise; even small errors can have a magnified effect due to the small base or height.
Can square footage be calculated if I only know angles and one side?
Yes, if you have enough angle and side information to define the triangle (e.g., Angle-Side-Angle, Side-Angle-Angle), you can use trigonometric formulas (e.g., Law of Sines) to find the missing base and height, or apply the formula Area = (1/2)ab sin(C) where a and b are known sides and C is the included angle.
How does the square footage of a triangular room affect heating and cooling calculations?
While square footage is a key input, heating and cooling calculations also consider ceiling height to determine cubic footage (volume), as well as window area, insulation values, and local climate. However, accurate floor square footage is the starting point for load calculations.
What's the difference between area and perimeter for a triangle?
Area (square footage) measures the two-dimensional space enclosed within the triangle. Perimeter measures the total distance around the outside edges of the triangle (sum of its three side lengths). They are distinct concepts.
How can I visually estimate the square footage of a triangular area for a quick idea?
Visually estimate the base and perpendicular height (e.g., by pacing). Then, mentally apply the 'half of base times height' formula. This provides a rough ballpark figure, useful for initial planning but not for material purchasing.
When should I consult a professional for triangle square footage calculations?
For very large, complex, or legally critical projects (e.g., land surveying, structural engineering, official property assessments), it's always best to consult a professional surveyor, architect, or engineer who has specialized tools and expertise for precise measurements.
How to calculate the surface area of a triangular object, like a piece of wood?
If it's a flat piece of wood, you're calculating its 2D area using Base × Height / 2. If it's a 3D object with triangular faces, you'd calculate the area of each triangular face and sum them up for the total surface area.
Are there standard waste factors for specific materials in triangular installations?
Waste factors can vary by material and project complexity. General guidelines are 5-10% for simple layouts, 10-15% for angled or complex layouts, and sometimes more for materials like tile with patterns or very large format pieces, but it's always best to check manufacturer recommendations.
How does the side length of a triangle relate to its overall area?
While side lengths define the triangle, the area is specifically determined by the base and its *corresponding perpendicular height*. Simply having long sides doesn't guarantee a large area if the height is very small, as seen in very narrow triangles.
Can I use grid paper to estimate triangular square footage?
Yes, for a rough estimate, you can draw your triangle on grid paper. Count the full squares inside and estimate the partial squares. This method is useful for visual approximation but is not precise enough for material ordering.
What's the role of square footage in a triangular room for furniture placement?
Knowing the square footage helps understand the usable floor area. More importantly, understanding the triangle's shape (base and height) and angles will guide practical furniture placement to avoid awkward layouts and maximize functionality.
How to convert square centimeters to square feet for small triangular areas?
First, calculate the area in square centimeters (cm²) using base and height in cm. Then, divide your cm² result by 929.03 (since 1 sq ft ≈ 929.03 sq cm).