Mastering the Trapezoid: Your Definitive Guide to Square Footage Calculation

Ever stared at a uniquely shaped room, a challenging garden plot, or a custom-designed patio and wondered, "How on earth do I measure that?" In a world dominated by perfect squares and rectangles, the humble trapezoid often presents a delightful, yet sometimes daunting, challenge. Whether you're a homeowner embarking on a DIY renovation, a landscaper envisioning a unique outdoor space, a contractor estimating materials, or simply a student grappling with geometry, accurately calculating the square footage of a trapezoid is a skill that proves invaluable in countless real-world scenarios.

From the charming sloped ceiling of an attic room to the precise cuts needed for a trapezoidal roof section, understanding how to determine the area of this four-sided polygon is crucial for budgeting, planning, and executing projects with precision. Without a clear method, you risk overspending on materials, miscalculating space, or facing unexpected hurdles down the line.

This comprehensive guide is designed to demystify the process of finding the square footage of a trapezoid. We'll break down the essential measurements – Base 1, Base 2, and Height – explaining each in simple terms. We'll then unpack the universal formula, providing intuitive explanations and detailed, step-by-step examples that you can easily follow for your own projects. Our aim is to equip you with the knowledge and confidence to tackle any trapezoid area calculation, making even the most unconventional shapes a breeze to measure. By the end of this article, you'll not only understand how to calculate trapezoid area, but also why each part of the formula is important, transforming a potentially confusing task into a straightforward one.

Understanding the Trapezoid: The Key Dimensions You Need

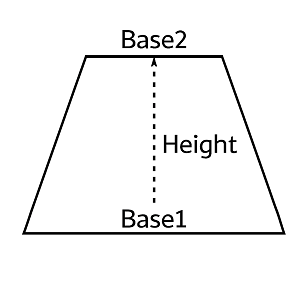
Before we dive into the calculations, it's essential to grasp what a trapezoid is and, more importantly, to correctly identify the specific measurements required for its area calculation. Unlike a simple rectangle or square where all sides are equal or opposite sides are parallel and equal, a trapezoid has a unique characteristic that defines it: it is a four-sided polygon (a quadrilateral) with at least one pair of parallel sides. This distinction is critical because these parallel sides are the 'bases' you'll use in your formula.

Imagine a table where the top surface is flat, but the legs angle outwards, making the bottom supports wider than the top. Or picture a basic house roof, where the eaves are wider than the ridge. These are common visual representations of trapezoids. The beauty of this shape is that its area can always be determined if you have three crucial pieces of information.

Let's break down these key dimensions:

1. Base 1 (b1) & Base 2 (b2): The Parallel Foundations

These are the stars of our calculation! Base 1 and Base 2 refer to the two sides of the trapezoid that are parallel to each other. In any given trapezoid, you will always have exactly one pair of parallel sides. It doesn't matter which one you label as 'Base 1' and which as 'Base 2' – the formula will work the same way because addition is commutative (the order doesn't change the sum).

• Identifying them: Look for the sides that, if extended indefinitely, would never meet. These are your parallel bases. In many diagrams, one might be at the top and the other at the bottom, but they could also be on the left and right if the trapezoid is rotated.
• Measurement Tips:
  • Consistency is Key: Ensure both bases are measured using the same unit (e.g., both in feet, both in inches, or both in meters). In construction and real estate, measurements are often in feet and inches, so converting everything to a consistent decimal foot measurement early on can prevent errors (e.g., 10 feet 6 inches becomes 10.5 feet).
  • Accuracy: Measure along the true length of the parallel side. For physical objects like rooms or garden beds, use a reliable tape measure. If dealing with blueprints or plans, read the specified dimensions carefully.

2. Height (h): The Perpendicular Bridge

This is arguably the most crucial and sometimes trickiest measurement for a trapezoid: the height (h). The height of a trapezoid is defined as the perpendicular distance between its two parallel bases.

• Understanding 'Perpendicular': This means the distance must be measured at a perfect 90-degree angle to both bases. Imagine dropping a straight line from any point on one base directly down to the other base – that line represents the height.
• Why it's NOT the Slant Side: A very common mistake is confusing the height with the length of the non-parallel (slant) sides of the trapezoid. These slant sides are almost always longer than the actual height, unless the trapezoid is a rectangle (where the height is the side length). Using a slant side instead of the perpendicular height will lead to a significantly inaccurate area calculation.
  • Think of it like this: if you push a rectangular box so it becomes slanted (a parallelogram or rhombus), its height (the distance between its parallel top and bottom) remains the same even if the side edges get longer due to the slant. The same principle applies here.
• Measurement Tips:
  • Using a Square: If measuring a physical object, use a carpenter's square, a T-square, or any tool that helps you establish a precise 90-degree angle from one base to the other.
  • Multiple Points: For larger areas, it's wise to measure the height at a couple of different points along the parallel bases to ensure your bases truly are parallel and your height measurement is consistent.
  • Consistent Units: Just like the bases, the height must be in the same unit of measurement. If your bases are in feet, your height must also be in feet.

Why these three inputs? These three measurements – Base 1, Base 2, and Height – uniquely define the total enclosed two-dimensional space of any trapezoid. With them, you have all the necessary information to precisely calculate its square footage, unlocking the blueprint for your next project, no matter its shape.

The Universal Trapezoid Area Formula: Unpacked

Now that we have a solid understanding of the essential components – Base 1 ($b_1$), Base 2 ($b_2$), and the perpendicular Height ($h$) – it's time to introduce the elegant and incredibly versatile formula that ties them all together. This formula is the cornerstone of trapezoid area calculation, and once you grasp its logic, you'll find it surprisingly intuitive.

The Formula at a Glance:

The universal formula for calculating the area of any trapezoid is:

Area = 1/2 × (Base1 + Base2) × Height

Or, expressed using the standard mathematical notations we discussed:

Area = 1/2 × (b1 + b2) × h

You might also see it written in a slightly different, but equivalent, way:

Area = (b1 + b2) / 2 × h

This second variation emphasizes that you're essentially finding the average length of the two parallel bases and then multiplying that average by the height. In fact, many find it helpful to think of it precisely that way:

Area = (Average of Bases) × Height

Regardless of which way it's written, the core operations remain the same, leading you to the accurate square footage of your trapezoidal shape.

Breaking Down the Formula: A Step-by-Step Logic

Let's dissect this formula piece by piece to understand why it works so effectively:

Step 1: Sum the Bases (b1 + b2)

The very first step is to add the lengths of your two parallel bases. But why do we do this? Imagine if you had a rectangle. Its area is simply length times width. A trapezoid, however, isn't a rectangle; it's like a rectangle that has been "tilted" or "stretched" on one side. By adding the two parallel bases, you're gathering information about both the shorter and longer parallel boundaries of your shape. This sum begins the process of finding an "effective" or "average" base length that accounts for the varying lengths of the two parallel sides.

Step 2: Divide by Two (1/2 or (b1 + b2)/2)

Once you have the sum of the two bases, the next crucial step is to divide that sum by two. This action yields the average length of the two parallel bases. This 'average base' is a critical concept because it allows us to conceptually transform the trapezoid into an equivalent rectangle.

Intuitive Explanation: The "Rectangular Transformation"

To truly grasp why this formula works, let's use a simple, powerful analogy:

Imagine you have a trapezoid cut out of paper. Now, picture yourself cutting off the triangular "pointy" part from one of the non-parallel sides. If you carefully take that triangular piece and rotate it, then attach it to the other side of the trapezoid, what do you get? A perfect rectangle!

The length of this newly formed rectangle isn't the length of Base 1, nor is it the length of Base 2. Instead, its length is precisely the average of Base 1 and Base 2. The width of this newly formed rectangle remains the original height of the trapezoid, because you only moved parts horizontally, not vertically.

So, the area of this "transformed" rectangle is its length (the average of the bases) multiplied by its width (the height). This simple visual trick demonstrates why averaging the bases is fundamental to the trapezoid area formula. It's a clever way to convert a complex shape into a simpler one that we already know how to measure.

Step 3: Multiply by the Height (× h)

Finally, you multiply the average length of the bases by the perpendicular height. Just as with a rectangle (length × width), this last multiplication gives you the total two-dimensional space enclosed by the trapezoid. It effectively "stretches" that average base length across the entire vertical span of the shape.

Units of Measurement: Ensuring Square Footage

Consistency in units is paramount to getting your final answer in 'square feet' (or square meters, or square inches, depending on your needs).

• If Base 1, Base 2, and Height are all measured in feet: Your calculated area will automatically be in square feet. For example, if b1 = 10 ft, b2 = 14 ft, and h = 8 ft:

  Area = (10 ft + 14 ft) / 2 × 8 ft

  Area = 24 ft / 2 × 8 ft

  Area = 12 ft × 8 ft

  Area = 96 square feet (ft²)

• If your measurements are in inches: You can perform the calculation to get square inches, then divide by 144 (since 1 square foot = 12 inches × 12 inches = 144 square inches) to convert to square feet. It's generally recommended to convert all measurements to feet before applying the formula to avoid this extra conversion step and potential errors.
• If your measurements are in meters: Your calculated area will be in square meters (m²). If you need to convert to square feet, remember that 1 square meter is approximately 10.764 square feet.

Understanding this formula is not just about memorizing it; it's about appreciating the elegant geometric principle it represents. With your inputs correctly identified and this formula in hand, you're now ready to tackle any trapezoid area calculation with confidence and precision.

Step-by-Step Calculation Guide with Examples

Understanding the trapezoid and its formula is the first hurdle cleared. Now, let's put that knowledge into action with practical, step-by-step examples. These scenarios are designed to cover common situations you might encounter, from measuring a room to calculating materials for a garden bed, and will highlight how to handle different units of measurement.

The Formula Reminder:
Area = (Base1 + Base2) / 2 × Height
Or simply: Average of Bases × Height

Let's dive in!

Example 1: Simple Residential Room – Flooring Calculation

Imagine you have a uniquely shaped living area or an attic bedroom that isn't a perfect rectangle. Instead, two of its parallel walls measure differently, forming a classic trapezoid. You want to install new flooring and need to know the exact square footage of the room.

• Problem: A room has two parallel walls. One measures 10 feet long (Base 1) and the opposite parallel wall measures 14 feet long (Base 2). The perpendicular distance between these two walls (the Height) is 8 feet.
• Goal: Calculate the square footage of the room.

Step-by-Step Calculation:

1. Identify your inputs:
   • Base 1 (b1) = 10 feet
   • Base 2 (b2) = 14 feet
   • Height (h) = 8 feet
   • Self-check: Are all units consistent? Yes, all are in feet.
2. Sum the bases:
   • b1 + b2 = 10 ft + 14 ft = 24 ft
   • Interpretation: The total length of your parallel boundaries is 24 feet.
3. Find the average of the bases:
   • (b1 + b2) / 2 = 24 ft / 2 = 12 ft
   • Interpretation: The average effective base length of your trapezoid is 12 feet. This is the length of the equivalent rectangle we mentally form.
4. Multiply the average base by the height:
   • Area = 12 ft × 8 ft = 96 square feet
   • Result: The room's square footage is 96 sq ft.

Application: When buying flooring, you'll need approximately 96 square feet of material. It's always wise to add 5-10% for cuts and waste, so you might purchase around 101 to 106 square feet.

Example 2: Landscaping Project – Converting Units for a Garden Bed

You're planning a beautiful raised garden bed with a unique trapezoidal shape to fit a specific corner of your yard. You've measured everything in inches, but you need to order soil and mulch in cubic yards (which requires knowing square feet first).

• Problem: A garden bed has parallel sides measuring 120 inches (Base 1) and 96 inches (Base 2). The perpendicular distance between these two parallel sides (the Height) is 72 inches.
• Goal: Calculate the square footage of the garden bed.

Step-by-Step Calculation:

1. Crucial First Step: Convert all measurements to feet! This is a common pitfall. Performing calculations in inches and then converting the final large area number can lead to errors if the conversion factor (144 square inches per square foot) isn't correctly applied. It's almost always safer to convert your linear measurements first.
   • Base 1 (b1): 120 inches ÷ 12 inches/foot = 10 feet
   • Base 2 (b2): 96 inches ÷ 12 inches/foot = 8 feet
   • Height (h): 72 inches ÷ 12 inches/foot = 6 feet
2. Identify your converted inputs:
   • Base 1 (b1) = 10 feet
   • Base 2 (b2) = 8 feet
   • Height (h) = 6 feet
3. Sum the bases:
   • b1 + b2 = 10 ft + 8 ft = 18 ft
4. Find the average of the bases:
   • (b1 + b2) / 2 = 18 ft / 2 = 9 ft
5. Multiply the average base by the height:
   • Area = 9 ft × 6 ft = 54 square feet
   • Result: The garden bed's square footage is 54 sq ft.

Application: Knowing this area is the first step to calculating the volume of soil needed. If your garden bed is 1 foot deep, you'd need 54 cubic feet of soil, which you could then convert to cubic yards for ordering.

Example 3: Irregular Trapezoid (Identifying Parallel Sides) – Plot of Land Calculation

Sometimes, a shape might look irregular, but if it has at least one pair of parallel sides, it's a trapezoid! This example focuses on correctly identifying those parallel sides.

• Problem: You are reviewing a property deed for a small plot of land that is not rectangular. It has four sides with lengths: 20 meters, 15 meters, 18 meters, and 10 meters. The survey indicates that the 20-meter side and the 10-meter side are parallel. The perpendicular distance between these two parallel sides is 12 meters.
• Goal: Calculate the area of the land plot in square meters, then convert it to square feet.

Step-by-Step Calculation:

1. Crucial Step: Correctly identify the parallel bases! The problem explicitly states that the 20m and 10m sides are parallel. The 15m and 18m sides are the slant (non-parallel) sides and are not used in the base calculation.
   • Base 1 (b1) = 20 meters
   • Base 2 (b2) = 10 meters
   • Height (h) = 12 meters
   • Self-check: All units are consistent (meters).
2. Sum the bases:
   • b1 + b2 = 20 m + 10 m = 30 m
3. Find the average of the bases:
   • (b1 + b2) / 2 = 30 m / 2 = 15 m
4. Multiply the average base by the height:
   • Area = 15 m × 12 m = 180 square meters
   • Result (in meters): The land plot's area is 180 sq m.
5. Convert to Square Feet (if needed for context, e.g., real estate in imperial regions):
   • Remember: 1 square meter ≈ 10.764 square feet
   • Area in sq ft = 180 sq m × 10.764 sq ft/sq m ≈ 1937.52 square feet
   • Result (in feet): The land plot's area is approximately 1937.52 sq ft.

Application: This calculation is vital for property valuation, zoning compliance, or planning any construction on the land.

Example 4: Construction Scenario – Dealing with Decimals for a Foundation Section

Precision is key in construction. You're laying out a concrete foundation for a building extension, and one section is trapezoidal, requiring precise material ordering.

• Problem: A foundation section has parallel bases measuring 22.5 feet (Base 1) and 18.75 feet (Base 2). The measured perpendicular height between these bases is 15.2 feet.
• Goal: Calculate the square footage of this foundation section.

Step-by-Step Calculation:

1. Identify your inputs:
   • Base 1 (b1) = 22.5 feet
   • Base 2 (b2) = 18.75 feet
   • Height (h) = 15.2 feet
   • Self-check: All units are consistent (feet), including decimals.
2. Sum the bases:
   • b1 + b2 = 22.5 ft + 18.75 ft = 41.25 ft
3. Find the average of the bases:
   • (b1 + b2) / 2 = 41.25 ft / 2 = 20.625 ft
4. Multiply the average base by the height:
   • Area = 20.625 ft × 15.2 ft = 313.5 square feet
   • Result: The foundation section's square footage is 313.5 sq ft.

Application: This exact square footage would be used to calculate the volume of concrete needed for this section, by multiplying it by the desired thickness of the slab.

These examples illustrate the versatility and straightforwardness of the trapezoid area formula once you correctly identify your inputs and maintain consistent units. With practice, you'll be able to apply this calculation to any real-world trapezoidal shape you encounter.

Real-World Applications of Trapezoid Area

The ability to calculate the square footage of a trapezoid isn't just an abstract mathematical exercise; it's a practical skill that unlocks solutions to a wide array of real-world problems. From home improvement projects to professional construction and beyond, understanding this geometric calculation can save you time, money, and frustration. Let's explore some of the most common and impactful applications:

Home Improvement & DIY Projects:

• Flooring: Many rooms aren't perfect rectangles or squares. Attics, additions, and even living rooms can have angled walls, creating trapezoidal shapes. Accurately calculating the square footage ensures you purchase the correct amount of tiling, carpeting, hardwood, laminate, or any other flooring material, minimizing waste and preventing costly under-ordering.
• Painting: When tackling a painting project, particularly in rooms with sloped ceilings or walls (common in attics or under staircases), calculating the area of the trapezoidal wall sections is essential for estimating the amount of paint needed. This prevents you from buying too much (and wasting money) or too little (and having to make an inconvenient second trip to the store).
• Roofing: Roofs often have complex shapes. Calculating the square footage of trapezoidal sections is crucial for estimating the number of shingles, tiles, or other roofing materials required. This is a critical step in both DIY roof repairs and large-scale roofing projects.
• Garden Beds: Designing a unique and visually appealing garden often involves creating non-rectangular planting areas. Trapezoidal raised garden beds, for example, can add interest and functionality to your landscaping. Knowing the square footage allows you to accurately calculate the amount of soil, mulch, and edging materials needed.
• Patio Construction: Building a patio that perfectly fits your outdoor space might involve creating a trapezoidal shape. Calculating the square footage ensures you order the right amount of pavers, concrete, or other materials, preventing both shortages and excessive leftovers.

Construction & Architecture:

• Foundation Layouts: Buildings aren't always simple rectangles. Sections of a foundation, especially for additions or oddly shaped properties, might be trapezoidal. Precise square footage calculations are essential for accurate concrete ordering and ensuring structural integrity.
• Wall Framing for Pitched Roofs: The framing of walls that support a pitched roof often involves trapezoidal sections. Calculating the area of these sections is vital for accurate lumber estimates and ensuring proper structural support.
• Estimating Materials for Concrete Slabs: For non-rectangular concrete slabs, like driveways or walkways with angled sections, calculating the trapezoidal areas is crucial for determining the volume of concrete needed. This prevents over- or under-pouring, which can be costly and time-consuming to correct.
• Unique Architectural Features: Modern architecture often incorporates unique shapes. Calculating the square footage of trapezoidal elements, such as angled windows, decorative panels, or custom-designed walls, is essential for accurate material estimation and construction planning.

Land Management & Surveying:

• Calculating Acreage of Irregularly Shaped Land Parcels: Property lines rarely follow perfect rectangles. Surveyors often need to calculate the area of trapezoidal sections of land to determine the total acreage, which is crucial for property valuation, zoning compliance, and legal descriptions.
• Determining Irrigation Needs: For agricultural or landscaping purposes, knowing the square footage of a trapezoidal field or garden allows for accurate calculation of water requirements and efficient irrigation system design.

Manufacturing & Engineering:

• Calculating Surface Area for Coatings: In manufacturing, calculating the surface area of trapezoidal components is necessary for accurately estimating the amount of paint, sealant, or other coatings needed.
• Material Cutting: When cutting materials like fabric, metal, or wood into trapezoidal shapes, knowing the square footage allows for efficient material usage and minimizes waste.

These examples demonstrate the wide-ranging applicability of the trapezoid area formula. From everyday DIY tasks to complex professional projects, mastering this calculation empowers you to work with precision and efficiency.

Tips for Accurate Measurement & Common Pitfalls

While the trapezoid area formula is straightforward, its accuracy hinges entirely on the precision of your measurements. Even small errors in measuring Base 1, Base 2, or especially the Height, can lead to significant discrepancies in your final square footage. Here are critical tips to ensure accuracy and common pitfalls to avoid:

• Measure Multiple Times: This cannot be stressed enough. Always measure each dimension (Base 1, Base 2, and Height) at least twice, and ideally, have someone else verify your measurements if possible. If your readings differ, re-measure until you get consistent results. This simple step can prevent costly errors down the line, whether you're ordering flooring or pouring concrete.
• Maintain Consistent Units: This is a recurring theme for a reason – it's a frequent source of error. Before you even touch the calculator, ensure all your linear measurements (Base 1, Base 2, and Height) are in the same unit. If you're aiming for square feet, convert any inches or other units to feet first. Remember, 1 foot = 12 inches. So, 6 inches becomes 0.5 feet, and 10 feet 3 inches becomes 10.25 feet.
• Correctly Identify Parallel Sides: A common mistake is to mistakenly use non-parallel sides as Base 1 and Base 2. Always confirm that the two sides you're labeling as bases are indeed parallel. If they're not, the shape isn't a simple trapezoid for this calculation, and you might need to break it down into multiple simpler geometric figures (like rectangles and triangles).
• The Height MUST Be Perpendicular: This is the most crucial aspect of measurement. The height is not the length of a slanted side. It must be the shortest, straight-line distance between the two parallel bases, forming a perfect 90-degree angle with them. Use a carpenter's square, a speed square, or a right-angle tool to ensure your measuring tape is perfectly perpendicular when you take this measurement. Measuring along a sloping side will always give you an inflated and incorrect area.
• Account for Obstructions: When measuring rooms or plots, be mindful of doorways, built-in cabinets, or other obstructions that might affect the usable square footage. You might need to calculate the area of the entire trapezoid first, then subtract the area of any non-usable sections.
• Consider Irregular Shapes: If your "trapezoid" isn't perfectly regular – meaning the parallel sides are clear, but the non-parallel sides are bowed, or there are significant cut-outs – the basic formula might not be enough. For truly irregular shapes, you might need to:
  • Divide and Conquer: Break the complex shape into simpler trapezoids, rectangles, and triangles. Calculate the area of each component and sum them up.
  • Grid Method: For very irregular shapes, overlay a grid of known unit squares (e.g., 1 ft x 1 ft) onto a scaled drawing and count the squares to estimate the area.
• Utilize Online Calculators as a Double-Check: After you've done your manual calculations, input your measurements into a reputable online trapezoid area calculator. This can serve as a quick verification step, helping you catch any arithmetic errors.

By paying meticulous attention to these details, you'll significantly increase the accuracy of your trapezoid square footage calculations, leading to more successful projects and precise estimations.

Beyond the Basics: Related Concepts & Advanced Considerations

While the formula for trapezoid area (Area = (b1 + b2) / 2 × h) is your primary tool, understanding its place within the broader world of geometry and real-world scenarios can deepen your expertise.

• Trapezoids vs. Other Quadrilaterals: It's helpful to remember that a trapezoid is one type of quadrilateral (a four-sided polygon). Other common quadrilaterals include squares, rectangles, and parallelograms.
  • A square is a special type of rhombus and a special type of rectangle, where all sides are equal and all angles are 90 degrees. Its area is simply side × side.
  • A rectangle is a parallelogram with all 90-degree angles. Its area is length × width.
  • A parallelogram is a quadrilateral with two pairs of parallel sides. Its area is base × height, which is fundamentally similar to the trapezoid formula if you consider the average base of a parallelogram to just be its single base.
  The trapezoid formula is unique because it specifically addresses the varying lengths of its parallel sides.
• Trapezium vs. Trapezoid (A Note on Nomenclature): If you encounter the term "trapezium," be aware that its meaning can vary by region. In American English, a "trapezoid" has one pair of parallel sides, and a "trapezium" has no parallel sides. However, in British English, it's often the other way around: a "trapezium" has one pair of parallel sides, and a "trapezoid" has no parallel sides. Always clarify the definition if you're working with international documents or software.
• Calculating Volume with Trapezoidal Bases: In three dimensions, a trapezoidal prism or trapezoidal solid has parallel trapezoidal bases. To calculate the volume of such a shape (like a trench with sloped sides, a concrete culvert, or a retaining wall), you first calculate the area of the trapezoidal base using the formula we've discussed. Then, you multiply that area by the length or depth of the prism. For example, Volume = (Trapezoid Area) × Length/Depth. This shows how knowing the 2D area is often the first step in more complex 3D calculations.

By understanding these related concepts, you gain a more complete picture of how trapezoid area calculations fit into a broader mathematical and practical context, preparing you for even more complex challenges.

Conclusion – Mastering Trapezoid Area for Your Projects

You've now journeyed through the intricacies of calculating the square footage of a trapezoid, transforming what might have seemed like a daunting task into a manageable skill. We've uncovered the true nature of this versatile shape, broken down its universal area formula, walked through practical, step-by-step examples, highlighted its many real-world applications, and armed you with crucial tips for accuracy.

Remember, the power of this calculation lies in correctly identifying your two parallel bases and the precise perpendicular height between them. With these three inputs, the formula — Area = (Base1 + Base2) / 2 × Height — becomes your reliable tool for estimating materials, planning layouts, and ensuring the precision of your projects.

From installing flooring in an unconventional room to laying out a custom garden bed or accurately assessing a unique property plot, the ability to determine trapezoid square footage is a valuable asset in your practical toolkit. Embrace the challenge of these unique shapes, knowing you now possess the knowledge to measure them accurately. Go forth, measure with confidence, and bring your geometrically precise projects to life!